30 60 90 Üçgeni Kuralı Nedir? 30 60 90 Üçgeninin Özellikleri Nelerdir?

Geometride en çok bilinen ve aynı zamanda en çok kullanılan üçgenler içerisinde 30-60-90 üçgeni gelmektedir. Bu üçgen aynı zamanda sabit formül üzerinden kenarları daha kolay bulma olanağı vermektedir. Aynı zamanda 30-60-90 üçgeni bir dik üçgen olarak da öne çıkar. Böylece üçgenin alanı ile beraber çevresi basit bir biçimde bulunabilmektedir. Sadece genel geometri değil aynı zamanda analitik geometri ve matematik problemleri üzerinden de kullanılan önemli bir sabit üçgen olarak öne çıkıyor.


30 60 90 Üçgeni Kuralı Nedir?
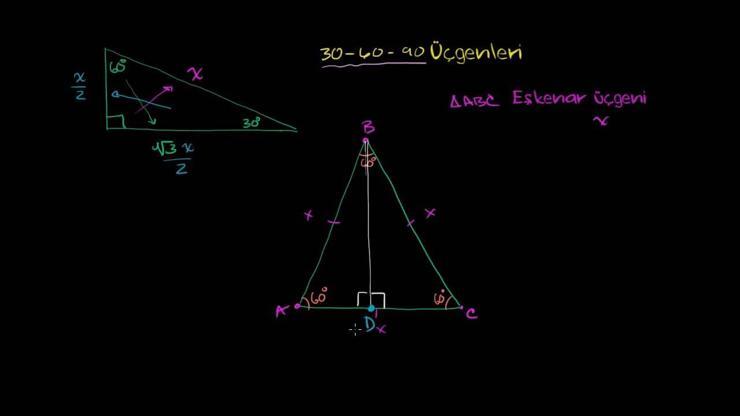
30 60 90 üçgeni kuralı bir dik üçgen üzerinden ele alınan sabit bir üçgendir. 30 derecenin karşısında olan kenar hipotenüs uzunluğunun yarısına verir. 60 derecenin karşısında olan kenar ise, 30 derecenin gördüğü kenar üzerinden kök 3 ile çarpılır. Aynı şekilde 90 derecenin karşısında olan kenar ise, 30 derecenin karşısındaki kenarının 2 katı olarak ifade edilmektedir. Bu şekilde sabit bir yapı ile beraber 30-60-90 üçgeni üzerinden Kural doğrultusunda kenarlar ve açılar kolayca bulunabilir.
30 60 90 Üçgeninin Özellikleri Nelerdir?
Belirli bir sabit ve kural doğrultusunda öne çıkan 30-60-90 üçgeni, geometrideki en önemli üçgenler içerisinde yer almaktadır. Bu bağlamda belli başlı bazı özellikleri ön plana çıkıyor.


- İç açıları her daim kural doğrultusunda 30-60-90 üçgeni olarak bilinir.
- Bir dik üçgendir.
- 30 derecenin karşısında olan kenar hipotenüsün yarısıdır.
- 60 derecenin karşısında olan kenar 30 dereceyi gören kenarın kök 3 katıdır.
- 90 derecenin karşısında olan kenar 30 derecenin önündeki kenarının iki katıdır.
- İç açıları toplamı 180 derecedir.
Bu şekilde öne çıkan özellikleri ve kuralları ile beraber, geometride birçok farklı işlem yapma olanağı tanımaktadır.
30-60-90 Üçgeni Nerelerde Kullanılır?
30-60-90 üçgeni özellikle üçgen içerisindeki hem açı hem de kenarı bulma konusunda büyük kolaylık sağlar. Aynı zamanda özellikle herhangi bir geometrik şekil doğrusunda, ortaya çıkarılan 30-60-90 üçgeni üzerinden alan kolayca bulunabilir. Aynı zamanda analitik geometri üzerinde de birçok farklı işlem yapma imkanı sağlayan bir yapıya sahiptir. Sabit kenarı ve açıları ile beraber, geometride oldukça fazla kullanılan üçgenler arasında yer alıyor.


SON DAKİKA
EN ÇOK OKUNANLAR


AGS sınav başvuru tarihi 2025: MEB Akademi Giriş Sınavı başvurusu ne zaman?

Son Dakika! LGS 2025 Başvuru ve Sınav Süreci: En Çok Merak Edilen 11 Soru ve Yanıtları

MEB NİSAN TATİL TAKVİMİ 2025: Nisan ara tatil ne zaman başlıyor, ne zaman bitiyor?

AUZEF VİZE SINAV TARİHLERİ 2025: AUZEF bahar dönemi ara sınavı ne zaman?

MEB 2. DÖNEM ORTAK SINAV TARİHLERİ 2025: MEB ortak sınavları hangi tarihlerde yapılacak?










